Introduction
2POL (Double Polarimeter) is a small-scale experiment in Mainz, Germany, to study quantum spin correlations of relativistic electrons.
Almost everyone is familiar with the elementary particle such as the electron. It has small mass and moves with relativistic velocities (comparable to the velocity of light) already at moderate energies.
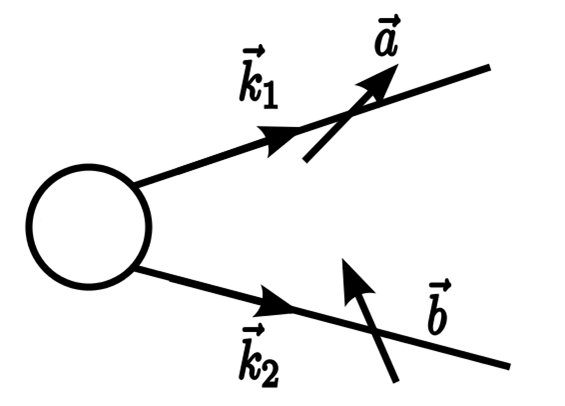
The electron, apart from its mass and elementary charge, possesses the spin which can be naively understood as an internal angular momentum. In quantum mechanics (QM) the spin is measured in terms of the Planck constant and amounts to ½ ℏ for the electron. The spin ½ may have only two projections on a given direction in space: + ½ or – ½ . Consider an event when two electrons leave an interaction region in which they were created in a certain quantum state and with momenta k1 and k2 , as shown in the figure below. Subsequently, a distance away, spin projections of both electrons are measured on assumed but arbitrary directions, respresented by the vectors „a” and „b”. There may be four results for each pair of such measurements, when spin projections have the following signs: ++,+ -, – +,- – . Determining probabilities of these four outcomes, p++ , p— , p+- , p-+ , is the basis of a correlation measurement (obviously, the sum of these probabilities equals 1). The electrons in general can be „entangled” which means that having left the interaction region they do not become fully independent one from another. That is to say, they are „correlated”. The fundamental quantity describing correlations quantitatively is called the correlation function, C, and in our case is expressed by the probabilities as follows: C = p++ + p— – (p+- + p-+ ) .
The idea of quantum spin correlations dates back to 1935 and a review of the subject can be found in the bookmark „Correlations”. Here we continue presenting the main features of the 2POL project.
Firstly, how to prepare a state „decaying” into two massive relativistic particles whose spin projections can be subsequently measured? After lengthy considerations we decided to scatter elestically electrons, i.e. use the Møller scattering to obtain a two-electron final state. This choice is a kind of a compromise – although correlations are more pronounced in a pure singlet state, whose creation in a relativistic domain seemed to be impossible – the simplest case of the Møller scattering may be realised when an electron beam is incident on a low-Z solid state target (here: Be) and the beam electrons scatter on the atomic electrons (nuclear scattering being the main source of background here). In this case the two outgoing electrons emerge from the state being a statistical mixture of a singlet and a triplet. Relativistic conditions are assured when the beam has energy of a few MeV and the symmetrically scattered Møller electrons – a half of this value.
Spin projections of MeV-electrons can be measured using the method of Mott polarymetry which can be explained simply as follows. An electron passing in the vicinity of a high-Z nucleus (Au in our case) is deflected in its Coulomb field. When it is incident „on the right” of the nucleus it is deflected to the left and if „on the left” – to the right. Two detectors are mounted symmetrically teen-centimetres from the Au target detecting electrons scattered at 120 degrees (our choice). The difference between scattering the „to the left” and „to the right” is such that the deflection proceeds with angular momentum vectors of opposite signs. This fact leads to a small asymmetry in the numer of counts recorded in the counters, one compared to the other, after a fair number of electrons has been counted. The quantity „asymmetry” in physics is generally defined as a difference of two quantities divided by their sum (here: numbers of events in one and the other counter). Asymmetry in the Mott scattering is related to the spin projection on the direction perpendicular to the scattering plane of the incident electron and the so called effective Sherman function proper for a given target material, its thickness, electron energy and scattering angle:
asymmetry = Sherman function (effective) ∙ spin projection .
Spin projection can be determined from this formula provided the asymmetry is measured and the effective Sherman function for the specific experimental conditions is known (simulated or measured in a dedicated experiment). Obviously, the higher is the value of the effective Sherman function, the better.
What are the Sherman function and the effective Sherman function? If the scattering occurs on a single nucleus (in other words, on a „one atom thick” target) then the Sherman function is the proper quantity. It can be calculated theoretically with arbitrary accuracy and the original paper is due to Sherman. The best known numerical implementation of the calculations is ELSEPA. The contour plot of the Sherman function presented below was obtained using results of this package. It can be seen from this plot that the function reaches high values of 0.5 – 0.6 but for large scattering angles where the Mott cross section is low.
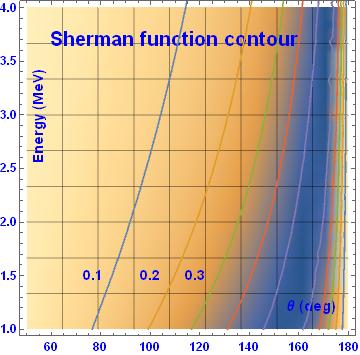
The effective Sherman function decreases with target thickness, starting from the theoretical value for a single nucleus. On the other hand the number of events scattered at a given angle increases proportionally with target thickness altogether implying that there is an optimal value for it, guided by optimum of the statistical uncertainty of the asymmetry. For example, for our February 2020 measurements with a 3 MeV electron beam (1.5 MeV symmetric Møller electrons) the optimal Au target thickness for scattering at 120 degrees is about 8 µm (10 µm used) and the effective Sherman funcgtion of approx. 0.1.
Measuring principle
The measurement proceeds as follows. The polarised 3 MeV beam electron scatters on an atomic electron in the Be target and we select events of a symmetrical scattering in the horizontal plane, each having the energy around 1.5 MeV. The outgoing electrons travel some 15 cm along the Møller leg towards Au targets of the respective Mott polarimeter, L and R (left and right). In each Mott polarimeter two counters are positioned in two arms, L and R, allowing to select those which are backscattered at 120 degrees to the left or to the right w.r.t. the Møller leg direction. Events contributing to the statistical sample for the correlation measurement are then such that: the electron going into the left Møller leg is counted in the left or right Mott arm and the electron going into the right Møller leg is counted in the left or right Mott arm. We thus have two possibilities of detection in the left Mott polarimeter and again two in the right Mott polarimeter and the overall number of combinations is 4. Having collected a large sample of all these events, we can determine frequencies of each combination or, after proper normalisation, experimental probabilities. The final quantities which we want to determine, p++ , p– – , p+- , p-+, can be derived from these experimental probabilities by a linear transformation whose 4 x 4 matrix has elements expressed by combinations of the Sherman function. Thus accuracy of the final results (the 4 numbers) depends critically on the precision with which the Sherman function is known.
In real life, all 4 counters record particles (mostly electrons but there may also be photons) of various energies. This means that the basic raw plot to be studied is the pulse height (pulse amplitude) distribution which can be related to energy of a particle through a procedure of calibration. The contribution from the Møller electrons of 1.5 MeV will correspond to a cusp and not a narrow line owing to the counter resolution. Since there is always background present in each counter, the art of counting the Møller electrons relies on its correct subtraction. This is done by way of collecting data with the Au target and without the Au target and taking the „difference” of the two in some way. This procedure allows to reject the background of external origin (not Au-related) leaving only that arising in the presence of the Au target (internal origin). With the external background rejected one can hope to determine the true number of Møller electrons in the resulting spectrum by adequately parametrising the internal background and thus selecting statistically the signal events.
Experimental setup
According to the above measurement idea, the technical project of the hardware of the 2POL detector follows logically this line. The left half of the detector is shown in the following figure (left Mott polarimeter and its two arms).

The beam enters from the right, the vertical tower near the red lead brick is a beam localiser screen target mechanism allowing to see the position of the beam spot (the screen target is moved upwards for data taking). The quasi-triangular block is the Møller piece with the 100 µm Be target immediately at the entry. The pipe continuing towards the left edge of the picture is the beam dump pipe with an absorber at the end to catch all beam electrons since only a small fraction of them interacts on the Be target. The scattered electrons go in all directions; we are interested in those which enter the Møller leg – a short pipe linking the Møller block and the left Mott polarimeter block. Again, the large-diameter pipe continuing towards the left bottom corner of the picture is the Møller dump pipe to absorb Møller electrons since, one more time, only a small fraction of them is backscattered on the Mott Au target, placed inside the Mott block of a hexagonal shape. The electrons are scattered in all directions but of interest for us are those entering one of the two Mott arms; the right arm is pointing towards the top edge of the picture while the left one goes underneath the red brick. The heavy lead blocks, identified by long screws sticking out of them, serve as a dedicated shielding for the scintillation counters in a heavy background accelerator environment. Here the plane spanned by the Mott arms is tilted w.r.t. to the horizontal plane by 45 degrees. The 2POL was not equipped with the right Mott polarimeter for the test study when the picture was taken.
Sensitivity
The main obstacle in the way to a precise result of our measurement is scarce statistics. We expect one counted double electron event per approximately 1017 beam electrons which corresponds to about 1/hour in the MAMI conditions. At this stage of the experiment (February 2020) it is too early to predict the precision to be achieved for the probabilities but an aim is about 10-20 %.
Financial support
The project is financially supported by the following institutions:
- National Science Centre (Poland)
- DAAD Deutsche Akademische Austauschdienst / Polish Ministry of Science and Higher Education
- University of Warsaw (Faculty of Physics)
- University of Łódź (Faculty of Physics and Applied Informatics)
- Technische Universitaet Darmstadt (Institut fuer Kernphysik)
The experiment is hosted by MAMI (Mainzer Mikrotron) at the Johannes Gutenberg Universitaet Mainz, where beam time, infrastructure and accelerator expertise is provided.